Area Related to Circles

Solved Questions on Area Related to Circles

1. The area of a minor sector of a circle with a radius of 8 cm and a central angle of 45° is:

a) 42 cm²
b) 12 cm²
c) 85 cm²
d) 27 cm²

Answer: b) 25.12 cm²

Explanation: The formula to calculate the area of a minor sector is

A = (θ/360) x π x r², where θ is the central angle and r is the radius of the circle. Substituting the given values, we get (45/360) x π x 8² = (1/8) x π x 64 = 8π = 25.12 cm² (approx.).

2. The area of a major sector of a circle with a radius of 10 cm and a central angle of 300° is:

a) 131.42 cm²
b) 162.83 cm²
c) 252.36 cm²
d) 261.66 cm²

Answer: d) 261.66 cm²

Explanation: The formula to calculate the area of a major sector is A = (θ/360) x π x r², where θ is the central angle and r is the radius of the circle. Plugging in the values, we get (300/360) x π x 10² = (5/6) x 3.14 x 100 = 261.66 cm².

3. The length of an arc in a circle with a radius of 30 cm and a central angle of 120° is:

a) 10π cm
b) 20π cm
c) 30π cm
d) 40π cm

Answer: b) 20π cm.

Explanation: Using the same formula as above, we have

C = (120/360) x 2π x 30 = (1/3) x 2π x 30 = 20π cm.

4. What is the area of the major segment of a circle with a radius of 8 cm and a central angle of 60°?

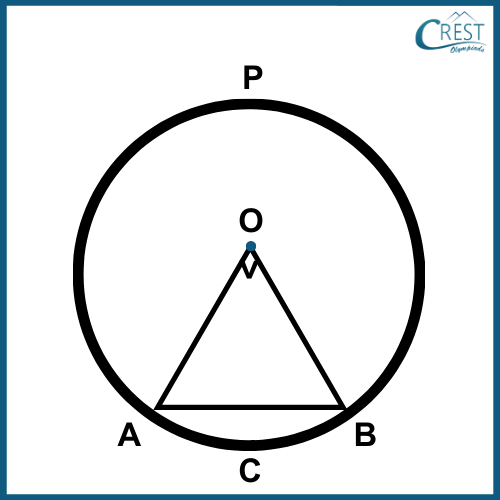
a) 181.059 cm²
b) 184.457 cm²
c)195.112 cm²
d) 206.458 cm²

Answer: c) 195.112 cm²

Explanation: The formula to calculate the area of the major segment is (θ₁/360) x π x r² + (1/2) x r² x sin(θ₂), where θ₁ is the angle of the major sector and θ₂ is the central angle of the triangle and r is the radius of the circle. So, θ₁ = 300°, θ₂ = 60° and r = 8 cm. Plugging in the values, we get (300/360) x π x 8² + (1/2) x 8² x sin (60°) = (5/6) x π x 64 + (1/2) x 64 x (√3/2) = 195.112 cm².

5. What is the area of a ring in a circle with an outer radius of 10 cm and an inner radius of 6 cm?

a) 12π cm²
b) 36π cm²
c) 50π cm²
d) 64π cm²

Answer: d) 64 cm²

Explanation: The formula to calculate the area of a ring is π (R² - r²), where R is the outer radius and r is the inner radius. Plugging in the values, we get π x (10² - 6²) = π x (100 - 36) = π x 64 = 64π cm².

Practice Questions on Area Related to Circles

1. The length of an arc in a circle is 15π cm. If the central angle of the arc is 60°, what is the radius of the circle?

a) 45 cm
b) 46 cm
c) 47 cm
d) 48 cm

Answer: a) 45 cm

2. The area of a ring in a circle is 33π cm². If the inner radius is 4 cm, what is the outer radius of the ring?

a) 6 cm
b) 7 cm
c) 10 cm
d) 12 cm

Answer: b) 7 cm

3. The central angle of an arc is 90°. If the length of the arc is 12π cm, what is the radius of the circle?

a) 13 cm
b) 18 cm
c) 21 cm
d) 24 cm

Answer: d) 24 cm

4. The length of an arc in a circle is 24π cm. If the radius of the circle is 18 cm, what is the central angle of the arc?

a) 60°
b) 190°
c) 240°
d) 310°

Answer: c) 240°

5. The area of a minor sector of a circle is 54π cm². If the central angle of the sector is 60°, what is the radius of the circle?

a) 23 cm
b) 18 cm
c) 16 cm
d) 12 cm

Answer: b) 18 cm

6. The area of a circle is 154π cm². What is the radius of the circle approximately?

a) 7 cm
b) 10 cm
c) 11 cm
d) 13 cm

Answer: d) 13 cm

7. The circumference of a circle is 30π cm. What is the radius of the circle?

a) 5 cm
b) 10 cm
c) 15 cm
d) 20 cm

Answer: c) 15 cm.

8. What is the area of a ring with an outer radius of 13 cm and an inner radius of 12 cm?

a) 196π cm²
b) 207π cm²
c) 305π cm²
d) 344π cm²

Answer: b) 207π cm²

9. What is the area of the triangle formed by a sector of a circle with a central angle of 45° and a radius of 6 cm?

a) 9 cm²
b) 12 cm²
c) 18 cm²
d) 24 cm²

Answer: c) 18 cm²

10. The central angle of a sector in a circle is 60°. If the area of the triangle formed by the sector is 12 cm², what is the radius of the circle?

a) 2 cm
b) 3 cm
c) 4 cm
d) 6 cm

Answer: a) 2 cm