Worksheet on Electricity for Class 10

1. A workshop uses a set of power tools. The table below shows the power ratings of each tool and the hours they are used daily:

If the electricity rate is $0.10 per kWh, what is the total monthly cost of operating these tools?

a) $12.00
b) $19.80
c) $21.30
d) $24.60

Answer: c) Step 1: Calculate the daily energy consumption for each tool.

Circular Saw: 1200 W x 2 hours = 2400 Wh = 2.4 kWh
Drill: 800 W x 4 hours = 3200 Wh = 3.2 kWh
Angle Grinder: 1500 W x 1 hour = 1500 Wh = 1.5 kWh

Step 2: Calculate the total daily energy consumption for all tools.

Total daily energy consumption = Energy consumed by Circular Saw + Energy consumed by Drill + Energy consumed by Angle Grinder
Total daily energy consumption = 2.4 kWh + 3.2 kWh + 1.5 kWh = 7.1 kWh

Step 3: Calculate the monthly energy consumption.

Monthly energy consumption = Total daily energy consumption * Number of days in the month
Assuming there are 30 days in the month:
Monthly energy consumption = 7.1 kWh/day x 30 days = 213 kWh

Step 4: Calculate the total monthly cost.

The electricity rate is $0.10 per kWh.
Total monthly cost = Monthly energy consumption * Electricity rate
Total monthly cost = 213 kWh x $0.10/kWh = $21.30

 Therefore, the total monthly cost of operating these tools is $21.30.

2. In an electrical system, a substantial quantity of electric charge, precisely 80,000 coulombs, is transferred over a period of 30 minutes through a potential difference of 60 volts. Calculate the total amount of thermal energy produced during this process.

a) 48000 kJ
b) 4799 kJ
c) 1599 kJ
d) 2896 kJ

Answer: b) To calculate the heat produced (H) when 80,000 coulombs of charge (Q) is transferred in 30 minutes through a potential difference (V) of 60 volts, follow these steps:

1. Calculate the current (I):
I = Q/t
I = 80,000 C/30 x 60s
I = 44.4 A

2. Calculate the resistance (R) using Ohm's law:
R = V/I
R = 60 V/ 44.4 A
R = 1.35 Ω

3. Calculate the heat produced (H):
H = I² x R x t
H = (44.4 A)² x 1.35 Ω x (30 x 60 s)
H = 4799040.048 J

Converting to kilojoules:
H = 4799040.048 J/1000 = 4799 kJ

3. Determine the power dissipated by each resistor in the given circuit.

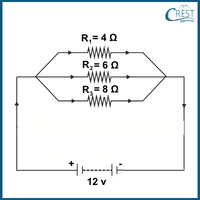
a) P₁: 48 W, P₂: 24 W, P₃: 96 W
b) P₁: 12 W, P₂: 18 W, P₃: 24 W
c) P₁: 16 W, P₂: 20 W, P₃: 36 W
d) P₁: 36 W, P₂: 24 W, P₃: 18 W

Answer: d) To calculate the power dissipated by each resistor in a parallel circuit connected to a 12V battery, we can use the formula for power:

P = I x V

Where:
P is the power in watts (W).
I is the current in amperes (A).
V is the voltage in volts (V).

Since all the resistors are connected in parallel to the same voltage source (12V battery), the voltage (V) is the same across all resistors. Therefore, we need to calculate the current (I) flowing through each resistor and then use that to calculate the power (P) for each resistor.

Using Ohm’s law, calculate the currents through each resistor:
I = V/R

Given:
R₁ = 4 Ω
R₂ = 6 Ω
R₃ = 8 Ω
V = 12 V

For R₁:
I₁ = V/R₁
I₁ = 12/4 = 3 A

For R₂:
I₂ = V/R₂
I₂ = 12/6 = 2 A

For R₃:
I₃ = V/R₃
I₃ = 12/8 = 1.5 A

Now that we have the currents through each resistor, we can calculate the power dissipated by each resistor using the formula
P = I x V

So, the power dissipated by each resistor in the parallel circuit is as follows:

Power dissipated by R₁:
P₁ = I₁ x V
P₁ = 3 x 12 = 36 W

Power dissipated by R₂:
P₂ = I₂ x V
P₂ = 2 x 1₂ = 24 W

Power dissipated by R₃:
P₃ = I₃ x V
P₃ = 1.5 x 12 = 18 W

4. Consider the following circuit with three identical light bulbs. If bulb B burns out, what will be the brightness of bulb A and C compared to before?

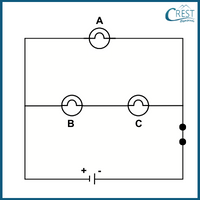
a) Bulb B and C will be brighter than before.
b) Bulb A will be the same, and C will be completely off.
c) Bulb A will be dimmer, and C will be the same as before.
d) Bulb A will be the same, and C will be dimmer than before.

Answer: b) In the given circuit, bulb A is in parallel with bulbs B and C, while bulbs B and C are in series. When bulb B burns out, the circuit becomes an open circuit in the series branch containing bulbs B and C.
Since bulb A is in parallel with the series branch of bulbs B and C, it will continue to receive the same voltage as before. Therefore, bulb A will remain at the same brightness as before. Since bulb B has burned out and there is no current flowing through the series branch, bulb C will also be off, and its brightness will be zero.

5. A copper wire has a resistance of 3 Ω. If a new copper wire is taken that has the same length as the first wire but has four times the cross-sectional area, what will be the resistance of the new wire?

a) 3 Ω
b) 12 Ω
c) 0.75 Ω
d) 0.18 Ω

Answer: c) The resistance of a wire is indeed inversely proportional to its cross-sectional area, assuming the length and resistivity remain constant. The formula for resistance is:

R = (ρ x L) /A

Given that the first copper wire has a resistance (R₁) of 3 ohms and the new copper wire has four times the cross-sectional area, we can compare their resistances using the ratio of their cross-sectional areas:

R₁/R₂ = ((ρ.L)/A₁)/((ρ.L)/A₂)

Since the length and resistivity are the same for both wires, they cancel out.

R₁/R₂ = A₂/A₁

3/R₂ = 4/1
R₂ = 3/4
R₂ = 0.75 Ω

So, the resistance of the new copper wire is 0.75 ohms.