1. The range of vision for a normal human eye is typically from the near point of about 25 cm to the far point, which is considered to be at infinity. If someone's near point is measured at 40 cm, what can be said about their vision?
a) They have myopia
b) They have hypermetropia
c) They have astigmatism
d) They have normal vision
Answer: b) The near point is the closest distance at which an individual with normal vision can focus on an object. It's typically around 25 centimetres. Hypermetropia (farsightedness) is a condition where a person can see distant objects more clearly than nearby objects. In hypermetropia, the near point is farther away than the normal near point of 25 centimetres. If someone's near point is measured at 40 centimetres, it means they have difficulty focusing on objects that are closer to them, which is a characteristic of hypermetropia.
2. Select the option that accurately describes the primary functions of the components of the eye shown in the picture:
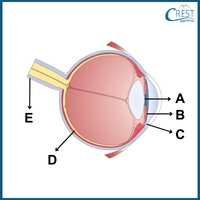
a) A: Pupil- Controls light intake, B: Ciliary Muscles- Shape the lens, C: Cornea- Focuses light onto the retina, D: Retina- Converts light to electrical signals, E: Optic Nerve- Transmits visual data to the brain
b) A: Iris- Adjusts pupil size, B: Ciliary Muscles- Shape the lens, C: Cornea- Focuses light onto the retina, D: Pupil- Controls light intake, E: Choroid- Supplies blood to the retina
c) A: Iris- Adjusts pupil size, B: Sclera- Protects and maintains eye shape, C: Pupil- Controls light intake, D: Retina- Converts light to electrical signals, E: Optic Nerve- Transmits visual data to the brain
d) A: Lens- Focuses on objects at varying distances, B: Iris- Adjusts pupil size, C: Cornea- Focuses light onto the retina, D: Retina- Converts light to electrical signals, E: Optic Nerve- Transmits visual data to the brain
Answer: d) A: The lens in the eye indeed helps focus on objects at different distances by changing its shape.
B: The iris controls the size of the pupil to regulate the amount of light entering the eye.
C: The cornea is responsible for focusing incoming light onto the retina.
D: The retina is a layer of tissue that contains photoreceptor cells (rods and cones) that convert light into electrical signals, which are then transmitted to the brain.
E: The optic nerve carries these electrical signals from the retina to the brain, where they are processed into visual information.
3. A beam of white light enters an equilateral prism, and the angle of incidence is 55 degrees. As the light emerges from the prism, it disperses into its constituent colours due to the phenomenon of dispersion. If the angle of emergence for violet light is 35 degrees, what would be the angle of deviation?
a) ∠D = 150o
b) ∠D = 60o
c) ∠D = 30o
d) ∠D = 35o
Answer: c) To find the angle of deviation (δ) for white light passing through an equilateral prism with an angle of incidence (i1) of 55 degrees and an angle of emergence for violet light (i2) of 35 degrees, we can use the formula: ∠D = ∠i + ∠e - ∠A
Where,
∠D: Angle of deviation
∠i: Angle of incidence = 55 degrees
∠e: Angle of emergence for violet light = 35 degrees
∠A: Angle of the prism = 60 degrees for an equilateral prism
Plugging in the values,
∠D = 55o+ 35o−60o
∠D = 30o
So, the angle of deviation for white light passing through the prism is 30 degrees.
4. When designing a traffic signal system, why is it important to consider the dispersion of light in the signal's design, particularly in regions with extreme weather conditions?
a) Dispersion affects the visibility of the signal from a distance.
b) Dispersion makes the signal change colours unpredictably.
c) Dispersion causes signal bulbs to overheat.
d) Dispersion is irrelevant in traffic signal design.
Answer: a) In regions with extreme weather conditions, such as heavy rain, fog, or snow, visibility can be significantly reduced. Dispersion of light, which causes the separation of colours, can affect the contrast and brightness of the signal. Proper signal design must account for dispersion to enhance visibility, ensuring that drivers can see and react to the signal from a distance even in adverse weather conditions.
5. A person with myopia has a far point at 50 cm. What would be the nature and the power of the lens required to correct their vision?
a) Nature of the lens: Concave; Power of the lens: 2 D
b) Nature of the lens: Concave; Power of the lens: -2 D
c) Nature of the lens: Convex; Power of the lens: 2 D
d) Nature of the lens: Convex; Power of the lens: -2 D
Answer: b) For myopia (nearsightedness), distant objects cannot be seen clearly because they are focused in front of the retina. To correct this, a concave lens is used to diverge incoming light.
The myopic person's far point is at 50 cm, which implies that they can perceive distant objects clearly when the image of these distant objects is created at their far point, located at a distance of 50 cm from their eye.
So,
Object distance, u = Infinity
Image distance, v = – 50 cm (in front of lens)
Using the lens formula to calculate the focal length of the concave lens required:
1/f = 1/v -1/u
1/f = 1/-50 - 1/Infinity
1/f = 1/-50 - 0 (1/Infinity = 0)
F = -50 cm
Therefore, the focal length of the necessary concave lens is -50 cm or 0.5 m.
To find the power (P) of the concave lens,
P = 1/f (in metres)
P = 1/-0.5
P = -2 diopters (D)
Hence, the nature of the lens required to correct the myopia is a concave lens, and its power is -2 diopters (D).


