Solved Questions on Number System and Polynomials
1. Which of the following is a rational number?
a) 5 + √3
b) 7 − √2
c) 8 + √4
d) 10 − √5
Answer: c) 8 + √4
Explanation: The root of the numbers like √2, √3 and √5 are irrational numbers.
The sum of a rational number and an irrational number and the difference between a rational number and an irrational number is an irrational number. Hence, 5 + √3, 7 − √2 and 10 − √5 are irrational numbers.
The sum of two rational numbers is a rational number.
Number: 8 + √4 = 8 + √(2 x 2) = 8 + 2 = 10 = 10/1
8 + √4 is a rational number which is in the form 101 where both ‘10’ and ‘1’ are integers and ‘1’ is not equal to zero.
2. Out of the following polynomials, which polynomial has the highest degree?
a) −8x5 + 4x3 − 3x + 2
b) 4x4 + 2x3 + x2 − 1
c) 7x5 + 3x4 − 2x3 + 4x2 − 5x + 1
d) 12x7 + 4x6 − 2x5 + 7x4 + 3x3 − 8x2 + 4x + 3
Answer: d) 12x7 + 4x6 − 2x5 + 7x4 + 3x3 − 8x2 + 4x + 3
Explanation: The degree of a polynomial is determined by the highest exponent of the variable within the expression.
The degree of the polynomial −8x5 + 4x3 − 3x + 2 is 5.
The degree of the polynomial 4x4 + 2x3 + x2 − 1 is 4.
The degree of the polynomial 7x5 + 3x4 − 2x3 + 4x2 − 5x + 1 is 5.
The degree of the polynomial 12x7 + 4x6 − 2x5 + 7x4 + 3x3 − 8x2 + 4x + 3 is 7.
Thus, the polynomial 12x7 + 4x6 − 2x5 + 7x4 + 3x3 − 8x2 + 4x + 3 has the highest degree.
3. When divided by (x + 3), the polynomials 3x3 + (p + 8)x2 + 16x − 6 and x3 − x2 − px + 15 leave the same remainder. What is the value of p?
a) 7
b) 5
c) 6
d) 2
Answer: a) 7
Explanation: The Remainder Theorem states that if you divide a polynomial f(x) by x−c, where c is a constant, the remainder will be f(c).
When x = −3,
For polynomial 3x3 + (p + 8)x2 + 16x − 6,
R1 = 3(−3)3 + (p + 8)(−3)2 + 16(−3) − 6
R1 = −81 + (p + 8)(9) − 48 − 6
R1 = −81 + 9p + 72 − 54
R1 = 9p - 63
For polynomial x3 − x2 − px + 15,
R2 =(−3)3 − (−3)2 − p(−3) + 15
R2 = −27 − 9 + 3p + 15
R2 = 3p − 21
Since R1 = R2
→ 9p − 63 = 3p − 21
→ 9p − 3p = −21 + 63
→ 6p = 42
→ p = 42/6
→ p=7
4. If a + b + c=8, then what is the value of (a − 3)3 + (b − 1)3 + (c − 4)3.
a) 0
b) 3
c) 3(a − 3)(b − 1)(c − 4)
d) (a − 3)(b − 1)(c − 4)
Answer: c) 3(a − 3)(b − 1)(c − 4)
Explanation: a + b + c = 8
(a − 3) + (b − 1) + (c − 4)=0
Let A = a − 3, B = b − 1 and C = c − 4
A + B + C=0
We know that if a + b + c=0, then a3 + b3 + c3=3abc
Thus, A3 + B3 + C3 = 3ABC
(a − 3)3 + (b − 1)3 + (c − 4)3 = 3(a − 3)(b − 1)(c − 4)
5. Using the law of exponents, simplify: 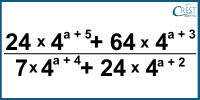
a) 224/17
b) 228/17
c) 220/17
d) 232/17
Answer: a) 224/17
Explanation: We know that if a, b, m and n are real numbers, then: