Worksheet on Quadratic and Linear Equations for Class 10

Solved Questions on Quadratic and Linear Equations

1. What is the solution of the following pair of linear equations 5x + y = 10 and 10x − 7y = 50?

a) x = − ⁸⁄₃ and y = $\frac{\frac{\mathrm{10}}{}}{\frac{3}{}}$
b) x = − ⁸⁄₃ and y = − $\frac{\frac{\mathrm{10}}{}}{\frac{3}{}}$
c) x = ⁸⁄₃ and y = $\frac{\frac{\mathrm{10}}{}}{\frac{3}{}}$
d) x = ⁸⁄₃ and y = − $\frac{\frac{\mathrm{10}}{}}{\frac{3}{}}$

Answer: d) x = ⁸⁄₃ and y = − $\frac{\frac{\mathrm{10}}{}}{\frac{3}{}}$

Explanation: We are given a pair of linear equations in two variables

5x + y = 10 … (1)

10x − 7y = 50 … (2)

Now, express the value of y in terms of x from the equation (1),

y = 10 − 5x … (3)

Now we substitute this value of y in Equation (2),

→ 10x − 7(10 − 5x) = 50

→ 10x − 70 + 35x = 50

→ 45x = 50 + 70

→ 45x = 120

→ x = ¹²⁰/₄₅

→ x = ⁸⁄3

Substitute this value of x = ⁸⁄₃ in equation (3) to find the value of y.

→ y = 10 − 5($\frac{\frac{8}{}}{\frac{3}{}}$)

→ y = 10 − $\frac{\frac{\mathrm{40}}{}}{\frac{3}{}}$

→ y = $\frac{\frac{\mathrm{30\; -\; 40}}{}}{\frac{3}{}}$

→ y = $\frac{\frac{\mathrm{-\; 10}}{}}{\frac{3}{}}$

Thus, x = ⁸⁄3 and y = −¹⁰⁄3

2. If and are the roots of the equation x² + 6x + 8 = 0, then which of the following equations has roots (α + β)² and (α - β)²?

a) x² − 144x + 40 = 0
b) x² + 144x − 40 = 0
c) x² + 40x − 144 = 0
d) x² − 40x + 144 = 0

Answer: d) x² − 40x + 144 = 0

Explanation: We are given x² + 6x + 8 = 0

Here, a = 1, b = 6 and c = 8

We know that the roots of the quadratic equation are given by

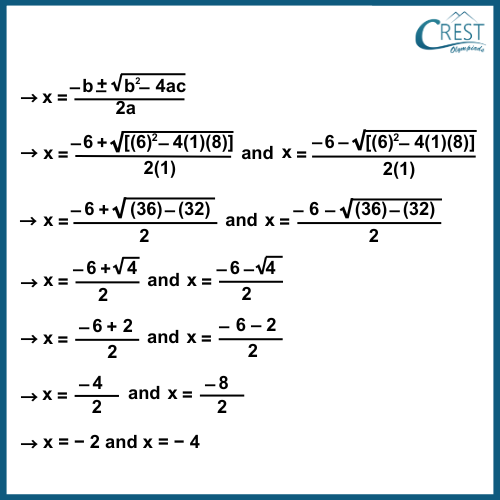
Thus, α = − 2 and β = − 4 are the roots of the given quadratic equation.

Now, α + β = − 2 + (− 4) = − 2 − 4 = − 6

→ (α + β)² = (- 6)² = 36

Also, α − β = − 2 − (− 4) = − 2 + 4 = 2

→ (α - β)² = (2)² = 4

We know that a quadratic equation is obtained by the formula

x² − (Sum of roots)x + Product of roots = 0

Thus, the quadratic equation with (α + β)² and (α - β)² as roots is:

→ x² − [(α + β)² + (α - β)²]x + [(α + β)² × (α - β)²] = 0

→ x² − [36 + 4]x + [36 × 4] = 0

→ x² − 40x + 144 = 0

3. The ratio between a two-digit number and the sum of digits of that number is 5 : 2. If the digit in the unit place is 4 more than the digit in the tenth place, then what is the number?

a) 25
b) 18
c) 15
d) 38

Answer: c) 15

Explanation: Let the digit in the tenth place be a and the digit in the unit place be b.

Hence, the number is 10a + b.

We are given that the ratio between a two-digit number and the sum of digits of that number is 5 : 2.

→ $\frac{\frac{\mathrm{10a\; +\; b}}{}}{\frac{\mathrm{a\; +\; b}}{}}$ = $\frac{\frac{5}{}}{\frac{2}{}}$

→ 2(10a + b) = 5(a + b)

→ 20a + 2b = 5a + 5b

→ 20a − 5a = 5b − 2b

→ 15a = 3b

→ b = $\frac{\frac{\mathrm{15a}}{}}{\frac{3}{}}$

→ b = 5a … (1)

We are also given that the digit in the unit place is 4 more than the digit in the tenth place.

→ b = a + 4 … (2)

Now, substitute the value of b = 5a in equation (2),

→ 5a = a + 4

→ 5a − a = 4

→ 4a = 4

→ a = $\frac{\frac{4}{}}{\frac{4}{}}$

→ a = 1

Putting the value of a in equation (1) to find the value of b,

→ b = 5(1)

→ b = 5

Thus, the required number = 10a + b = 10(1) + 5 = 15

4. For which values of p and q, will the following pair of linear equations

3x + 2y = 7 and (3p + 10q)x + (p + 4q)y = 2p − q + 1 have infinitely many solutions?

a) p = - 8/33 and q = 1/11
b) p = - 8/11 and q = 1/11
c) p = 8/33 and q = - 1/11
d) p = 8/11 and q = - 1/11

Answer: a) p = - 8/33 and q = 1/11

Explanation: We are given the pair of linear equations

3x + 2y = 7

(3p +10q)x + (p + 4q)y = 2p − q + 1

Here, a₁ = 3, a₂ = 3p + 10q, b₁ = 2, b₂ = p + 4q, c₁ = 7 and c₂ = 2p − q + 1

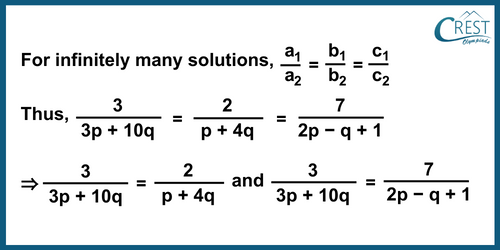
First solving,

($\frac{\frac{3}{}}{\frac{\mathrm{3p\; +\; 10q}}{}}$) = ($\frac{\frac{2}{}}{\frac{\mathrm{p\; +\; 4q}}{}}$)

→ 3(p + 4q) = 2(3p + 10q)

→ 3p + 12q = 6p + 20q

→ 3p − 6p = 20q − 12q

→ − 3p = 8q

→ p = ^-8⁄₃ q … (1)

Now solving,

($\frac{\frac{3}{}}{\frac{\mathrm{3p\; +\; 10q}}{}}$) = ($\frac{\frac{7}{}}{\frac{\mathrm{2p\; -\; q\; +\; 1}}{}}$)

→ 3 (2p − q + 1) = 7(3p + 10q)

→ 6p − 3q + 3 = 21p + 70q

→ 6p − 21p + 3 = 70q + 3q

→ − 15p + 3 = 73q … (2)

Substituting the value of p in equation (2)

→ − 15(^-8⁄3 q) + 3 = 73q

→ − 5(−  8q) + 3 = 73q

→ 40q + 3 = 73q

→ 40q − 73q = −  3

→ − 33q = −  3

→ q = ^-3⁄_-33

→ q = ¹⁄11

Now put the value of q in equation (1) to find the value of p

→ p = ^-8⁄₃ q
→ p = ^-8⁄₃ (¹⁄₁₁)
→ p = ^-8⁄₃₃

Hence, p = ^-8⁄33 and q = ¹⁄₁₁.

5. What is the value of ‘p’ if the product of roots of the given quadratic equation (p + 7)x² − (2p − 11)x + (3p − 4) = 0 is ¹³⁄₅?

a) 45.5
b) 55.5
c) 65.5
d) 75.5

Answer: b) 55.5

Explanation: We are given the quadratic equation (p + 7)x² − (2p − 11)x + (3p − 4) = 0

Here a = p + 7, b = − (2p − 11) and c = 3p − 4

We know that the product of roots of a quadratic equation = ^c⁄_a

Product of the roots the given quadratic equation = ¹³⁄₅

→ ($\frac{\frac{\mathrm{3p\; -\; 4}}{}}{\frac{\mathrm{p\; +\; 7}}{}}$) = ¹³⁄₅

→ 13 × (p + 7) = 5 × (3p − 4)

→ 13p + 91 = 15p − 20

→ 91 + 20 = 15p − 13p

→ 111 = 2p

→ p = ¹¹¹⁄₂

→p = 55.5