Worksheet on Chapter: Triangles and its Properties - Class 10

Solved Questions on Triangles and its Properties

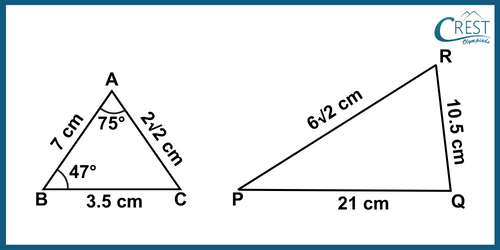
1. In △ABC, AB = 7 cm, BC = 3.5 cm, CA = 2√2 cm, ∠A = 75° and ∠B = 47° and in △PQR, PQ = 21 cm, QR = 10.5 cm, RP = 6√2 cm. What is the value of ∠P?

a) 75°
b) 47°
c) 58°
d) 68°

Answer: c) 58°

Explanation: We are given that in △ABC, AB = 7 cm, BC = 3.5 cm, CA = 2√2 cm, ∠A = 75° and ∠B = 47°.

In △PQR, PQ = 21 cm, QR = 10.5 cm, RP = 6√2 cm.

The figure is shown below:

According to SSS (Side-Side-Side) Similarity Criterion,

△ABC ~ △PQR

Thus, ∠C = ∠P     [Corresponding angles of the similar triangles]

We know that the sum of all angles of a triangle is 180°.

In △ABC,

∠A + ∠B + ∠C = 180°

75° + 47° + ∠C = 180°

122° + ∠C = 180°

∠C = 180° − 122°

∠C = 58°

Since ∠C = ∠P

∠P = 58°

2. Consider the following statements:

(i) If A and B are the points on the sides PQ and PR of △PQR such that
PQ = 21 cm, PA = 6 cm, BR = 20 cm and PB = 8 cm, then AB || QR.

(ii) If in △ABC and △PQR, ∠A = 38°, ∠B = 57°, ∠P = 85° and ∠Q = 57°, then △BAC ~ △RQP.

Out of the following, which statement is TRUE?

a) Only (i)
b) Only (ii)
c) Both (i) and (ii)
d) Neither (i) nor (ii)

Answer: a) Only (i)

Explanation:

Consider Statement (i): We are given PQ = 21 cm, PA = 6 cm, BR = 20 cm and PB = 8 cm

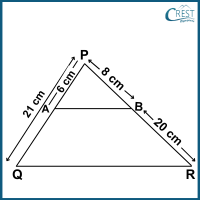
Thus, AQ = PQ − PA

AQ = 21 − 6

AQ = 15 cm

Now,  PA/AQ = 6/15 = 2/5

Also, PB/BR = 8/20 = 2/5 

PA/AQ = PB/BR 

The converse of basic proportionality theorem states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Thus, AB || QR

Thus, statement (i) is TRUE.

Consider Statement (ii):

We are given that in △ABC and △PQR, ∠A = 38°, ∠B = 57°, ∠P = 85° and ∠Q = 57°.

We know that the sum of all angles of a triangle is 180°.

Thus, in △ABC,

∠A + ∠B + ∠C = 180°
38° + 57° + ∠C = 180°
95° + ∠C = 180°
∠C = 180° − 95° 
∠C = 85° 

Now in △PQR,

∠P + ∠Q + ∠R = 180°
85° + 57° + ∠R = 180°
142° + ∠R = 180°
∠R = 180° − 142° 
∠R = 38°

Thus, in △BAC and △QRP,

∠A = ∠R = 38° 
∠B = ∠Q = 57° 
∠C = ∠P = 85° 

Thus, by AAA similarity

△BAC ~ △QRP

Thus, statement (ii) is FALSE.

Therefore, Only (i) is TRUE.

3. Consider the figure given below:

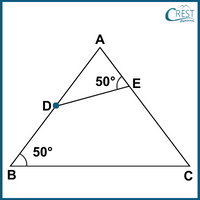
ABC is a triangle with ∠B = 50° and AB = 12 cm. ADE is another triangle with ∠AED = 50°, AD = 7 cm and AE = 5 cm. What is the length of EC?

11. a) 11. 5 cm
12. b) 11.75 cm
13. c) 11.6 cm
14. d) 11.8 cm

Answer: d) 11.8 cm

Explanation: The given figure is shown as:

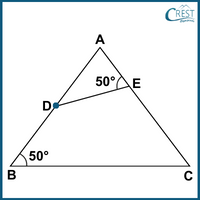
Let ∠A = θ

In △ABC and △AED,
∠BAC = ∠DAE (Common)
∠ABC = ∠AED = 50° (Given)

Thus, by AA similarity criterion, 

△ABC ~ △AED

AC / AD = AB / AE = BC / ED

Taking AC / AD = AB / AE

AC / 7 = 12 / 5
AC = (12 × 7) / 5
AC = 84 / 5

Now, AC = AE + EC

EC = AC − AE
= (84 / 5) − 5
= (84 − 25) / 5
= 59 / 5
= 11.8 cm

∴ EC = 11.8 cm

4. In a trapezium ABCD, AB || DC and DC = 3AB. EF drawn parallel to AB cuts AD at F and BC at E such that BE/EC = ?. If diagonal DB intersects EF at G, then which of the following is correct?

a) EF = 2AB
b) 9EF = 17AB
c) 9EF = 16AB
d) 9EF = 19AB

Answer: b) 9EF = 17AB

Explanation: The figure is shown below:

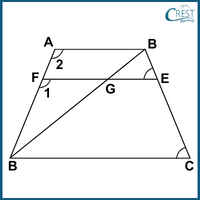
We are given that DC = 3AB and ^BE⁄_EC= 45

In △DFG and △DAB,

∠DFG = ∠DAB [Corresponding angles since AB || FG]
∠FDG = ∠ADB [Common]

We know that if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar by AA similarity criteria.

△DFG ~ △DAB    [By AA similarity]

Thus, ^DF⁄_DA = ^FG⁄_AB … (1)

In trapezium ABCD, AB || EF || CD

^AF⁄_FD = ^BE⁄_EC

But ^BE⁄_EC = ⁴⁄₅

^AF⁄_FD = ⁴⁄₅

Adding 1 on both the sides

^AF⁄_FD + 1 = ⁴⁄₅ + 1

^AF+FD⁄_FD = ⁴⁺⁵⁄₅

^AD⁄_FD = ⁹⁄₅

^FD⁄_AD = ⁵⁄₉ … (2)

From equation (1) and (2),

^FG⁄_AB = ⁵⁄₉

FG = ⁵⁄₉AB … (3)

In △BEG and △BCD,

∠BEG = ∠BCD [Corresponding angles since EG || CD]

∠GBE = ∠DBC [Common]

We know that if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar by AA similarity criteria.

△BEG ~ △BCD    [By AA similarity]

Thus, ^BC⁄_BE = ^EG⁄_CD

We know that ^BE⁄_EC = ⁴⁄₅

^EC⁄_BE = ⁵⁄₄

Adding 1 on both sides

^EC⁄_BE + 1 = ⁵⁄₄ + 1

^EC+BE⁄_BE = ⁵⁺⁴⁄₄

^EC⁄_BE = ⁹⁄₄

^BE⁄_EC = ⁴⁄₉

But ^BE⁄_BC = ^EG⁄_CD

^EG⁄_CD = ⁴⁄₉

EG = ⁴⁄₉CD

We know that CD = 3AB

EG = ⁴⁄₉(3AB)

EG = ¹²⁄₉AB                              … (4)

Adding equation (3) and (4),

FG + EG = ⁵⁄₉AB + ¹²⁄₉AB

EF = ¹⁷⁄₉AB

9EF = 17AB

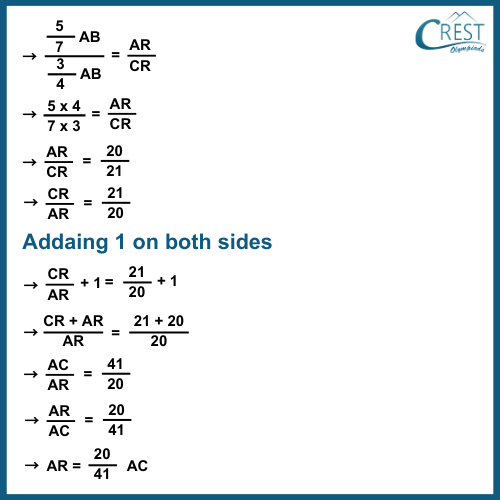
5. ABCD is a parallelogram in the given figure. AB is divided at P and CD at Q such that AP : PB = 5 : 2 and CQ : QD = 3 : 1. If PQ meets AC at R, then which of the following is true?

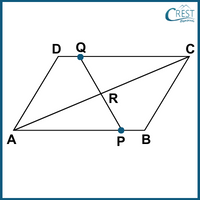
a) AR = ²¹⁄₄₀AC
b) AR = ²¹⁄₄₁AC
c) AR = ²⁰⁄₄₁AC
d) AR = ²³⁄₄₀AC

Answer: c) AR = ²⁰⁄₄₁AC

Explanation: In △APR and △CQR,

∠PAR = ∠QCR [Alternate interior angles since AB || CQ]

∠ARP = ∠CRQ [Vertically opposite angles]

We know that if two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar by AA similarity criteria.

△APR ~ △CQR    [By AA similarity]

^AP⁄_CQ = ^PR⁄_QR = ^AR⁄_CR … (1)

We are given that AP : PB = 5 : 2 

^AP⁄_AB = ^AP⁄_AP+PB
         = ⁵⁄₅₊₂
          = ⁵⁄₇

AP = ⁵⁄₇AB

We are given that CQ : QD = 3 : 1 

^CQ⁄_CD = ^CQ⁄_CQ+QD
          = ³⁄₃₊₁
           = 3⁄₄

CQ = 3⁄₄CD

Since ABCD is a parallelogram, its opposite sides are equal

AB = CD

CQ = 3⁄₄AB

From equation (1), we have

^AP⁄_CQ = ^AR⁄_CR

Substituting AP = 57AB and CQ = 34AB in the above equation