Solved Questions on Mensuration
1. Each rectangular tile is 50 centimetres long and 35 centimetres wide. How many tiles will be required to cover the floor of a room with a length of 9.45 metres and a breadth of 2.5 metres?
a) 115
b) 135
c) 155
d) 175
Answer: b) 135
Explanation: Length of the rectangular tile = 50 cm = 50/100 m = 0.5 m
Breadth of the rectangular tile = 35 cm = 35/100 m = 0.35 m
Area of the rectangular tile = Length × Breath = 0.5 m × 0.35 m
Length of the floor of a room = 9.45 m
Breadth of the floor of a room = 2.5 m
Area of the floor of a room = Length × Breath = 9.45 m × 2.5 m
Number of tiles = Area of the floor of a room/Area of the rectangular tile
= (9.45 m × 2.5 m)/(0.5 m × 0.35 m)
= (945 m × 25 m × 10 × 100)/(100 × 5 m × 35 m × 10)
= 135
2. Four regular hexagons of perimeter 300 cm each are joined. What is the perimeter of the new figure formed as shown in the given figure?
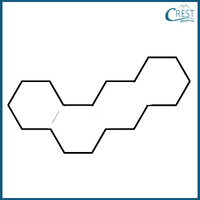
a) 300 cm
b) 600 cm
c) 900 cm
d) 1200 cm
Answer: c) 900 cm
Explanation: Perimeter of a regular hexagon = 300 cm
⇒ 6 × Side of a regular hexagon = 300 cm
⇒ Side = 300/6 cm
⇒ Side = 50 cm
The number of sides is marked in the figure.
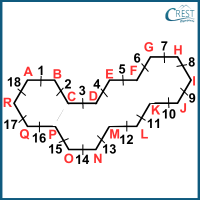
There are 18 equal sides in the figure.
Perimeter of the given figure = Sum of the lengths of sides of the figure
= AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LM + MN + NO + OP + PQ + QR + RA
= 18 × 50 cm
= 900 cm
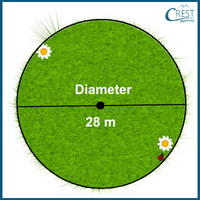
3. The diameter of a circular field is 28 metres. How much distance will a man walk in order to make eight complete rounds of this field?
a) 604 m
b) 624 m
c) 704 m
d) 724 m
Answer: c) 704 m
Explanation: Diameter (d) of a circle field = 28 m
One Complete round = Circumference of a circular field = πd
= 22/7 × 28
= 88 m
Total distance walked by man to complete 8 rounds = 8 × One Complete round
= 8 × 88 m
= 704 m
4. What is the length of each side of the field if the cost of fencing a square plot at the rate of $2.50 per metre is $2700?
a) 270 m
b) 540 m
c) 720 m
d) 1080 m
Answer: a) 270 m
Explanation: Total cost of fencing a square plot = $2700
Rate of fencing per metre = $2.50
Perimeter of square = Total cost of fencing a square plot / Rate of fencing
= 2700/ 2.5
= 1080 m
Using the formula, perimeter of a square = 4 × Length of a side of a square plot
⇒ 4 × Length of a side of a square plot = 1080 m
⇒ Length of a side of a square plot = 1080 m/4
⇒ Length of a side of a square plot = 270 m
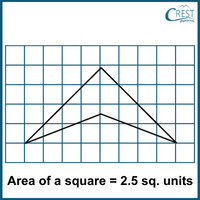
5. What is the total estimated area of the given figure?
a) 5 sq. units
b) 5 sq. units
c) 5 sq. units
d) 5 sq. units
Answer: b) 17.5 sq. units
Explanation: Area of a square = 2.5 sq. units
Number of completely covered squares = 2
Area of squares that are completely covered = 2 × 2.5 sq. units
= 5 sq. units
Number of squares which are more than half covered squares = 2
Area of squares that are more than half covered = 2 × 2.5 sq. units
= 5 sq. units
Number of squares which are exactly half covered square = ½ × 6 = 3
Area of squares that are exactly half covered square = 3 × 2.5 sq. units
= 7.5 sq. units
Number of squares which are less than half covered squares = 6
[Disregard any area that is less than half a square in size.]
Area of squares that are less than half covered squares = 0 sq. units
Total estimated area = 5 sq. units + 5 sq. units + 7.5 sq. units + 0 sq. units
= 17.5 sq. u





