Solved Questions on Mensuration
1. If the length and the breadth of a rectangular paper are 37 cm and 21 cm, what is the area of the largest circle which can be cut out of this paper?
a) 346.5 cm2
b) 537.82 cm2
c) 693 cm2
d) 1075.64 cm2
Answer: a) 346.5 cm2
Explanation: Length (l) of a rectangular paper = 37 cm
Breadth (b) of a rectangular paper = 21 cm
Largest circle which can be cut out of this paper with the largest diameter (d) is equal to the breadth (b) of a rectangular paper.
d = b
r = d/2 = b/2
= 21/2 cm
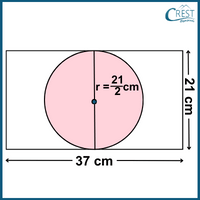
Area of a largest circle = 22/7 × (21/2)2 [Area of a circle = πr2, Where π = 22/7 ]
= 22/7 × (21/2) × (21/2)
= 346.5 cm2
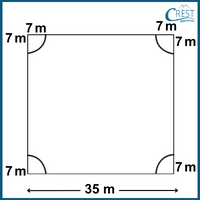
2. In a square field, a quarter of a circle with a radius of 7 cm is designated as a water pool starting from each of its corners. What is the area of the remaining part of the grassy area within the field if each side of the field is 35 m?
a) 1051 m2
b) 1061 m2
c) 1071 m2
d) 1081 m2
Answer: c) 1071 m2
Explanation: Area of a square field = a2 = 352 = 1225 m2
Four quadrants form a circle.
Area of four quadrants = Area of a circle [Area of a circle = πr2, Where π = 22/7]
= 22/7 × (7)2
= 22/7 × 7 × 7
= 154 m2
Area of the remaining part of the grassy area within the field
= Area of a square field − Area of four quadrants
= (1225 − 154) m2
= 1071 m2
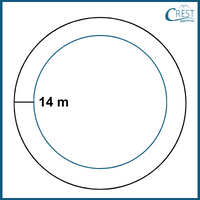
3. The circumference of a circular park is 264 metres and the width of the footpath around the park is 14 metres. what is the cost of fencing the outer circumference at the rate of $5.82 per metre?
a) $2028.24
b) $2028.64
c) $2048.24
d) $2048.64
Answer: d) $2048.64
Explanation: The figure is:
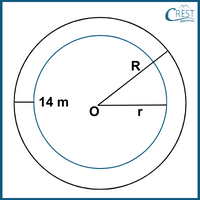
Inner circumference of a circular park = 264 m
⇒ 2πr = 264 m
⇒ 2 × 22/7 × r = 264 m [π = 22/7]
⇒ r = 264 × ½ × 7/22
⇒ r = 264 × ½ × 7/22
⇒ r = 42 m
Inner radius = r = 42 m
Outer radius = R = r + 14
= 42 + 14
= 56 m
Outer circumference of a footpath around a circular park = 2πR
= 2 × 22/7 × 56
= 352 m
Cost of fencing the outer circumference of 1 m = $5.82
Cost of fencing the outer circumference of 352 m = $5.82 × 352
= $2048.64
4. What is the total surface area of a cuboid if the side of a small cube is 3 cm?
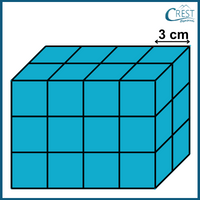
a) 428 cm
b) 448 cm
c) 468 cm
d) 488 cm
Answer: c) 468 cm
Explanation: Side of a small cube = 3 cm
Length (l) of a cuboid = 4 × Side of a small cube = 4 × 3 = 12 cm
Breadth (b) of a cuboid = 2 × Side of a small cube = 2 × 3 = 6 cm
Height (h) of a cuboid = 3 × Side of a small cube = 3 × 3 = 9 cm
Total surface area of a cuboid = 2(lb + bh + hl)
= 2(12 × 6 + 6 × 9 + 9 × 12)
= 2(72 + 54 + 108)
= 2 × 234
= 468 cm
5. The radius and height of the pig iron cylindrical roll are 49 centimetres and 484 centimetres, respectively. The pig iron is melted in the furnace and a huge cube is formed. What is the lateral surface of a cube formed?
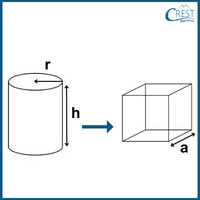
a) 7.5 m2
b) 9.5 m2
c) 11.5 m2
d) 13.5 m2
Answer: b) 9.5 m2
Explanation: r = 7 cm
h = 14 cm
Volume of cylinder = πr2h
= 22/7 × 492 × 484
= 22/7 × 49 × 49 × 22 × 22
= 22/7 × 49 × 49 × 22 × 22
= (22 × 22 × 22 × 7 × 7 × 7) cm3
Volume of an iron cube formed = Volume of cylinder
⇒ a3 = 22 × 22 × 22 × 7 × 7 × 7
⇒ a = 22 × 7
⇒ a = 154 cm
Lateral surface area = 4 × a2
= 4 × (154)2
= 4 × 154 × 154
= 94864 cm2
Lateral surface area in m2 = 94864/(100 × 100) m2
= 9.4864 m2
= 9.5 m2 [Round off]







