Worksheet on Triangles

Solved Questions on Triangles

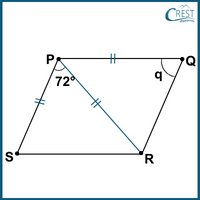
1. In the given quadrilateral PQRS, PQ = PR = PS, PR bisects ∠QRS and ∠RPS = 72°. What is the value of q?

a) 44°
b) 54°
c) 64°
d) 74°

Answer: b) 54°

Explanation: In the given quadrilateral PQRS,

PQ = PR = PS

PR bisects ∠QRS. Therefore, ∠PRQ = ∠PRS

∠RPS = 72°

In △PSR,

∠PRS + ∠PSR + ∠RPS = 180° (Angle Sum Property of a Triangle)

∠PRS + ∠PRS + 72° = 180° (PR = PS, ∠PSR = ∠PRS)

2∠PRS = 180° − 72°

2∠PRS = 108°

∠PRS = 54°

In △PQR,

∠PRQ = ∠PRS = 54° (PR bisects ∠QRS)

q = ∠PRQ = 54° (PQ = PR)

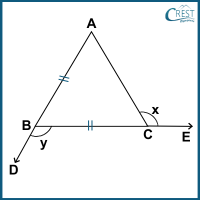
2. Which of the following options expresses x in terms of y?

a) x = 180° + y2
b) x = 180° − y2
c) x = 180° + 2y
d) x = 180° − 2y

Answer: b) x  = 180° − y2

Explanation: ∠ACB +  ∠ACE = 180° [Linear Pair]

∠ACB +  x = 180°
∠ACB = 180° − x

∠BAC = ∠ACB = 180° − x (Angle opposite to equal sides are equal, AB = BC)

∠ABC +  ∠CBD = 180° [Linear Pair]
∠ABC +  y = 180°
∠ABC = 180° − y

In ?ABC,
∠ACB + ∠BAC  + ∠ABC  = 180°     (Angle Sum Property of a Triangle)
180° − x + 180° − x  + 180° − y  = 180°
540° − 2x − y  = 180°
2x + y  = 540° − 180°
2x + y  = 360°
2x  = 360° − y
x  = ^360°-y⁄₂
x  = ^360°⁄₂ − ^y⁄₂
x  = 180° − ^y⁄₂

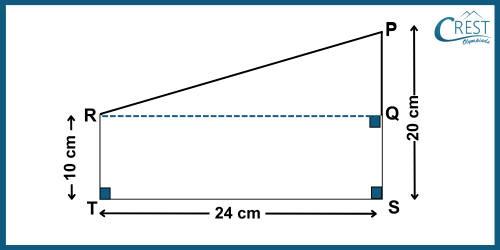
3. What is the length of PR using the information given in the figure?

a) 22 cm
b) 24 cm
c) 26 cm
d) 28 cm

Answer: c) 26 cm

Explanation: In △PQR,

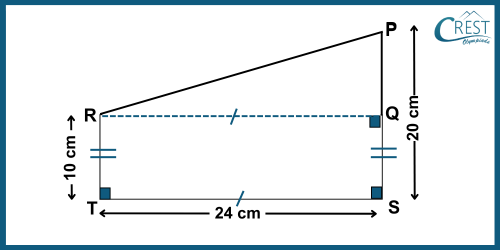
RQ = TS = 24 cm
PQ = PS − QS = PS − RT = 20 − 10 = 10 cm
PR2 = OD2 + OA2 [Pythagoras’ Theorem]
PR = √(RQ²+PQ²)
PR = √(24²+10²)
PR = √(576+100)
PR = √676
PR = √(26 × 26)
PR = 26 cm

4. In △XYZ, OZ bisects ∠Z and ∠OXZ = ∠OYZ. Which of the following is true?

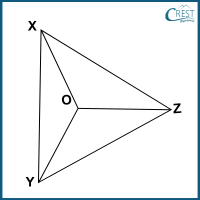
a) ∠XOZ = ∠YOZ; OX = OY; XY = YZ
b) ∠XOZ = ∠YZO; OX = OY; XZ = YZ
c) ∠XOZ = ∠YOZ; OX = OZ; XZ = YZ
d) ∠XOZ = ∠YOZ; OX = OY; XZ = YZ

Answer: d) ∠XOZ = ∠YOZ; OX = OY; XZ = YZ

Explanation: In △XOZ and △YOZ,

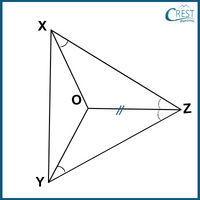
∠OXZ = ∠OYZ (Given)
OZ = OZ (Common)
∠OZX = ∠OZY  (OZ bisects ∠Z)
△XOZ ≅ △YOZ (A.S.A)
OX = OY  (Corresponding Parts of Congruent Triangles are Equal)
XZ = YZ  (Corresponding Parts of Congruent Triangles are Equal)
∠XOZ = ∠YOZ  (Corresponding Parts of Congruent Triangles are Equal)

5. The ratio between a base angle and the vertical angle of an isosceles triangle is 1 : 2. What is the value of each angle of the triangle?

a) Base Angle = 75° and Vertical Angle = 30°
b) Base Angle = 60° and Vertical Angle = 60°
c) Base Angle = 45° and Vertical Angle = 90°
d) Base Angle = 30° and Vertical Angle = 120°

Answer: c) Base Angle = 45° and Vertical Angle = 90°

Explanation: In △ABC,

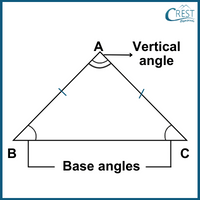
Base Angle : Vertical Angle =1 : 2

Let each base angle be x° and vertical angle be 2x°.
∠ABC = ∠ACB = x°   (Base Angles)
∠CAB = 2x°  (Vertical Angle)
∠ABC + ∠ACB + ∠CAB = 180° (Angle Sum Property of a Triangle)
x° + x° + 2x° = 180°
4x° = 180°
x° = 180°4
x° = 45°

Each Base Angle = ∠ABC = ∠ACB = x° = 45°

Vertical Angle = ∠CAB = 2x° = 2 × 45° = 90°