Solved Questions on Area of Parallelogram and Triangle
1. Which of the following is the correct option?
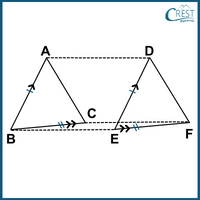
Based on the diagram, the following statements are stated below:
Statement A: Area (△ABC) is equal to Area (△DEF).
Statement B: The length of the side AC is parallel and equal to the length of the side DF.
Statement C: Area of parallelogram BCFE is equal to area parallelogram ADFC.
Statement D: Area (△FED) is equal to half of the area parallelogram BADE.
Statement E: Triangles CAB and FED lie on the same base AD and between the same parallels (DA and FC).
a) Only statements A, B, C and D are true.
b) Only statements A, C, D and E are true.
c) Only statements B, C, D and E are true.
d) All statements A, B, C, D and E are true.
Answer:d) All statements A, B, C, D and E are true.
Explanation: AB = DE and AB // DE
So, BADE is a parallelogram.
The labelled figure is:
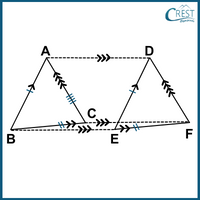
From theorems on Area of Parallelogram,
Area (//gm BCFE) = Area (//gm ADFC) = area (//gm BADE)
From theorems on Area of Triangle,
Area (△ABC) = Area (△DEF)
= 1⁄2 Area (//gm BCFE)
= 1⁄2 Area (//gm ADFC)
= 1⁄2 area (//gm BADE)
Triangles CAB and FED lie on the same base AD and between the same parallels (DA and FC). These triangles are congruent to each other. Hence, the length of the side AC is parallel and equal to the length of the side DF.
∴ Hence, all statements A, B, C, D and E are true.
2. A quadrilateral is described where the diagonals AC and BD intersect at right angles. The midpoints of its sides, denoted as P, Q, R and S, are connected to form segments PQ, QR, RS and SP. This results in a new quadrilateral PQRS. Which of the following is the correct option?
a) Quadrilateral PQRS is a parallelogram with PQ equal to RS.
b) Quadrilateral PQRS is a rectangle with PQ equal to RS.
c) Quadrilateral PQRS is a parallelogram with PR equal to QS.
d) Quadrilateral PQRS is a rectangle with PR equal to QS.
Answer:b) Quadrilateral PQRS is a rectangle with PQ equal to RS.
Explanation: A quadrilateral is described where the diagonals AC and BD intersect at right angles. The midpoints of its sides, denoted as P, Q, R and S, are connected to form segments PQ, QR, RS and SP. This results in a new quadrilateral PQRS.
The labelled figure is:
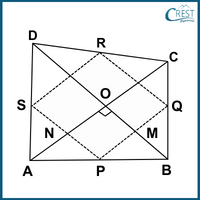
Using midpoint theorem:
In △ABC, P and Q are the mid-points of AB and BC, respectively.
PQ || AC and PQ = ½ AC ................. (i)
In △ADC, R and S are the mid-points of CD and AD, respectively.
RS || AC and RS = ½ AC ................. (ii)
Using (i) and (ii), we get
PQ || RS and PQ = RS
∴ In quadrilateral PQRS, a pair of opposite sides are equal and parallel. Hence, a quadrilateral PQRS is a parallelogram.
In △ABD, P is the midpoint of AB and S is the midpoint of AD.
PS || BD
⇒ PN || MO ................. (iii)
Using (i),
PQ || AC
⇒ PM || NO ................. (iv)
Using (iii) and (iv), we get
PN || MO and PM || NO
∴ In quadrilateral PNOM, two pairs of opposite sides are parallel. Hence, a quadrilateral PNOM is a parallelogram.
From the figure, the diagonals AC and BD of quadrilateral ABCD intersect at right angles.
∠NOM = 90°
In a parallelogram PNOM,
∠NPM = ∠NOM = 90° [Opposite angles of a parallelogram are equal.]
Hence, ∠SPQ = 90°.
Thus, PQRS is a parallelogram in which ∠SPQ = 90°.
∴ PQRS is a rectangle if one of the angles of a parallelogram is a right angle.
3. Which of the following is true if the medians of a triangle XYZ intersect at P?
a) Area (△XPZ) = 1⁄2 × Area (△XYZ)
b) Area (△XPZ) = 1⁄3 × Area (△XYZ)
c) Area (△XPZ) = 1⁄4 × Area (△XYZ)
d) Area (△XPZ) = 1⁄5 × Area (△XYZ)
Answer:b) Area (△XPZ) = 1⁄3 × Area (△XYZ)
Explanation:
As we know, the median of a triangle divides it into two triangles of equal area.
The labelled figure is:
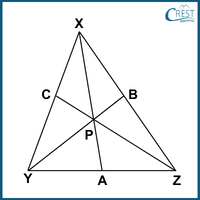
In △XYZ, XA is the median.
⇒ Area (△XAY) = Area (△XAZ) …….... (i)
In △YPZ, AP is the median
⇒ Area (△PAY) = Area (△PAZ) …….... (ii)
Subtracting (ii) from (i), we get
Area (△XAY) − Area (△PAY) = Area (△XAZ) − Area (△PAZ)
⇒ Area (△XPY) = Area (△XPZ) …….... (iii)
Similarly, In △XYZ, YB is the median.
⇒ Area (△XBY) = Area (△XBZ) …….... (iv)
In △YPZ, BP is the median
⇒ Area (△XPB) = Area (△ZPB) …….... (v)
Subtracting (iv) from (v), we get
⇒ Area (△XPY) = Area (△YPZ) …….... (vi)
From (iii) and (vi),
Area (△XPY) = Area (△XPZ) = Area (△YPZ) …….... (vii)
In △XYZ,
Area (△XPY) + Area (△XPZ) + Area (△YPZ) = Area (△XYZ)
Using (vii),
⇒ 3 × Area (△XPY) = Area (△XYZ)
⇒ Area (△XPY) = 1⁄3 × Area (△XYZ)
∴Area (△XPY) = Area (△XPZ) = Area (△YPZ) = 1⁄3 × Area (△XYZ)
4. ABCD is a trapezium in which the length of base CD is a cm, the length of AB is b cm and the length of AD is c cm. Which of the following is the correct option?
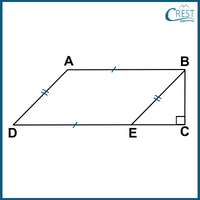
a) Area (△BEC) = 1⁄2 (a − b)√(a2 + b2 + c2 + 2ab)
b) Area (△BEC) = 1⁄2 (a − b)√(a2 + b2 + c2 − 2ab)
c) Area (△BEC) = 1⁄2 (a − b)√(a2 + b2 − c2 + 2ab)
d) Area (△BEC) = 1⁄2 (a − b)√(a2 + b2 − c2 − 2ab)
Answer:d) Area (△BEC) = 1⁄2 (a − b)√(a2 + b2 − c2 − 2ab)
Explanation: The labelled figure is:
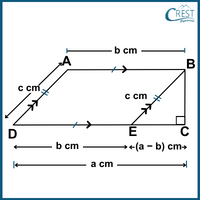
In △BEC,
BE = c cm
CE = (a − b) cm
BC = √(BE2− CE2)
= √(a − b)2− (c)2)
= √(a2 + b2− 2ab − c2)
= √(a2 + b2− c2− 2ab)
Area (△BEC) = 1⁄2 × Base × Height
= 1⁄2 × CE × BC
= 1⁄2 × (a − b) × √(a2 + b2− c2− 2ab)
5. Which statement is NOT true?
Statement A: Two triangles are said to be on the same base and between the same parallels if they have a common side and the vertex opposite to the common base of each figure lies on a line parallel to the base.
Statement B: Diagonals of a parallelogram divide it into four triangles of equal area.
Statement C: A median of a triangle divides it into three triangles of equal area.
Statement D: Two congruent parallelograms have equal areas but the converse need not be true.
a) Only statement A
b) Only statement B
c) Only statement C
d) Only statement D
Answer:c) Only statement C
Explanation:
A median of a triangle divides it into two triangles of equal area.







