Solved Questions on Euclid’s Geometry and Lines and Angles
1. Which of the following axioms states that if a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and the reverse is also true?
a) Adjacent angles axiom
b) Straight angles axiom
c) Linear pair axiom
d) Supplementary angles axiom
Answer: c) Linear pair axiom
Explanation: If a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and the reverse is also true. This property is known as the linear pair axiom.
2. Which of the following is NOT true for Euclid's postulates?
Postulate I: It is possible to draw a circle with any centre and diameter.
Postulate II: A straight line can be drawn from any given point to another point.
Postulate III: Lines that coincide with each other are equal.
Postulate IV: There is only one line that goes through both of them if there are two different points.
Postulate V: A terminated line can be extended infinitely.
a) Only I and II
b) Only II and III
c) Only III and IV
d) Only IV and V
Answer: c) Only III and IV
Explanation: III and IV are Euclid's axioms, not postulates.
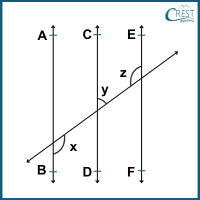
3. What is the value of angle z if AB || CD || EF and the angle y is one-third of angle x?
a) 120°
b) 128°
c) 135°
d) 144°
Answer: c) 135°
Explanation: In the given figure, x and z are alternate angles (AB || EF) and y and z are co-interior angles (CD || EF).
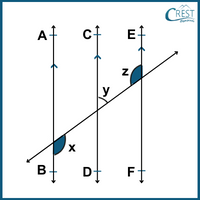
∠x = ∠z (alternate angles, AB || EF)
According to the question, ∠y = 1/3 ∠x
⇒∠y = 1⁄3 ∠z
∠y + ∠z = 180° (co-interior angles, CD || EF)
⇒ 1⁄3 ∠z + ∠z = 180°
⇒ 4/3 ∠z = 180°
⇒ ∠z = 180° × 3/4
∴ ∠z = 135°
Hence, ∠x = ∠z = 135°
4. Which of the following is true if AB || DE?
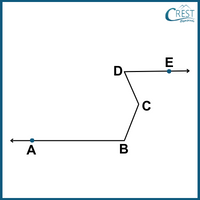
a) ∠ABC + ∠BCD + ∠CDE = 180º
b) ∠ABC + ∠BCD − ∠CDE = 180º
c) ∠ABC + ∠BCD + ∠CDE = 270º
d) ∠ABC + ∠CDE − ∠BCD = 180º
Answer: b) ∠ABC + ∠BCD − ∠CDE = 180°
Explanation: Draw a line CF through point C, making it parallel to both AB and DE.
Hence, AB || CF || DE. BC and CD are transversals.
The labelled diagram is shown as:
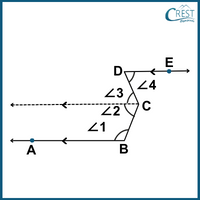
∠1 + ∠2 = 180° (Co-interior angles, AB || CF) ……………….(i)
∠3 = ∠4 (Alternate angles, CF || DE) ………………….(ii)
Adding (i) and (ii), we get:
∠1 + ∠2 + ∠3 = 180° + ∠4
⇒ ∠1 + (∠2 + ∠3) = 180° + ∠4
⇒ ∠ABC + ∠BCD = 180° + ∠CDE
∴ ∠ABC + ∠BCD − ∠CDE = 180º
5. What is the value of x, y and z if LI is parallel to ON, angle x is three-sevenths of the angle y and angle y is 1 times of angle z?
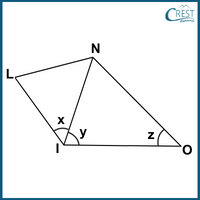
a) ∠x = 36°; ∠y = 72°; ∠z = 45°
b) ∠x = 36°; ∠y = 72°; ∠z = 60°
c) ∠x = 36°; ∠y = 84°; ∠z = 45°
d) ∠x = 36°; ∠y = 84°; ∠z = 60°
Answer: d) ∠x = 36°; ∠y = 84°; ∠z = 60°
Explanation: Angle x is three-sevenths of the angle y.
⇒ ∠x = 3/7 × ∠y
Angle y is 1 2⁄5 times of angle z.
⇒ ∠y = 1 2⁄5 × ∠z
⇒ ∠y = 7/5 × ∠z
∴ ∠z = 5/7 × ∠y
∠x + ∠y + ∠z = 180° (Co-interior angles, LI || ON)
⇒ (3/7 × ∠y) + ∠y + (5/7 × ∠y) = 180° [Put values of ∠x and ∠z in terms of ∠y]
⇒ (3/7 + 1 + 5/7) × ∠y = 180° [Take ∠y as common]
⇒ (3 + 7 + 5)/7 × ∠y = 180° [Take LCM as 7]
⇒ 15/7 × ∠y = 180°
⇒ ∠y = 180° × 7/15
∴ ∠y = 84°
∠x = 3/7 × ∠y
⇒ ∠x = 3/7 × 84°
∴ ∠x = 36°
∠z = 5/7 × ∠y
⇒ ∠z = 5/7 × 84°
∴ ∠z = 60°






