1. A cycle is travelling along a straight road. It accelerates from 2 ms-1 to 12 ms-1 in 5 seconds. At the same time, a car starts from rest and accelerates uniformly at 20 ms-2. After how much time will the car catch up to the cyclist?
a) 5.25 s
b) 5 s
c) 10 s
d) 2.45 s
Answer: b) To solve this problem, let's first calculate the distance covered by both the cycle and the car during the given time period, and then find out when they meet.
Given:
Initial velocity of the cyclist (u1) = 2 ms-1
Final velocity of the cyclist (v1) = 12 ms-1
Time (t1)= 5 seconds
Car's initial velocity (u2) = 0 ms-1 (starts from rest)
Car's acceleration (a2) = 20 ms-2
We want to find time t when the car catches up to the cyclist.
For the cyclist:
Using the following equation we can calculate the acceleration (a1) of the cyclist:
a1 = (v1 - u1)/t1
a1 = (12 ms-1 - 2 ms-1)/ 5 s
a1 = 2 ms-2
Using the second equation of motion we can calculate the distance travelled by the cyclist (s1):
s1 = u1 x t + 1/2 a1 x t2
s1 = 2 x t + 1/2 x 2 x t2
s1 = 2t x t2
For the car:
Using the second equation of motion we can find the distance travelled by car (s2):
s2 = u2 x t + 1/2 a2 x t2
s2 = 0 + 1/2 x 20 x t2
s2 = 10t2
Now, we can find the time t when the distances are equal:
s2 = s1
10t2 = 2t x t2
t = 5 s
The car will catch up to the cyclist after 5 seconds.
2. How does the velocity-time graph of an object in free fall (with constant acceleration due to gravity) appear?
a) 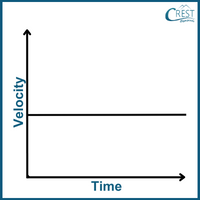
b) 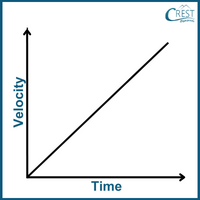
c) 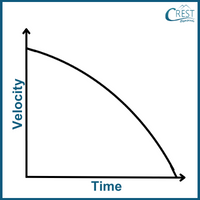
d) 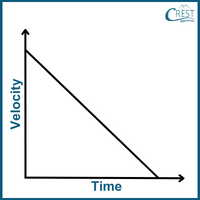
Answer: d) When an object is in free fall and experiencing constant acceleration due to gravity, its velocity changes uniformly over time. As the object falls, its velocity increases in the downward direction. This results in a straight line on a velocity-time graph with a negative slope as depicted by option d. The steeper the slope, the greater the acceleration due to gravity.
3. A train decelerates at a rate of 2 ms-2 and comes to a stop. If its initial velocity was 30 ms-1, how far does it travel during the deceleration?
a) 345 m
b) -225 m
c) 225 m
d) -60 m
Answer: c) To solve this problem, we can use the equation of motion that relates initial velocity, final velocity, acceleration, and distance:
Given:
Initial velocity (u) = 30 ms-1 (positive because it's in the forward direction)
Final velocity (v) = 0 ms-1 (the train comes to a stop)
Acceleration (a) = -2 ms-2 (negative because it's deceleration)
We need to find the distance (s) travelled during the deceleration.
We'll use the equation of motion:
v2 = u2 + 2as
Substitute the given values:
(0)2 = (302) + 2 x (−2) x s
0 = 900 − 4s
Solving for s:
4s = 900
s = 900/4
s = 225 m
So, the train travels a distance of 225 m during the deceleration.
4. A person is sitting in a train that's moving at a constant velocity. They toss a ball vertically upward. How does the ball's motion look to an observer outside the moving train?
a) The ball follows a curved path due to the train's motion.
b) The ball follows a straight vertical path upward and downward.
c) The ball follows a parabolic path upward and downward.
d) The ball's motion is unaffected by the train's velocity.
Answer: b) When the train is moving at a constant velocity, the person inside the train, as well as the ball they toss vertically upward, are also moving with that constant velocity. From the perspective of an observer outside the train, the ball's vertical motion is independent of the train's horizontal motion.
Gravity acts vertically downward on the ball, causing it to follow a straight vertical path upward and then downward. This is because the ball's motion is determined by the force of gravity and its initial upward velocity. The train's constant velocity does not influence the vertical motion of the ball, and it will appear to move vertically straight to an observer outside the train.
5. A Ferris wheel has a radius of 15 metres and completes one revolution in 60 seconds. Calculate the speed of a person sitting on the Ferris wheel at the outer edge.
a) 0.5 ms-1
b) 1.5 ms-1
c) 1 ms-1
d) 2 ms-1
Answer: b) To calculate the linear speed of a person sitting on the Ferris wheel at the outer edge, we can use the formula for calculating the velocity of an object undergoing uniform circular motion:
v = Circumference/Time taken
Given:
Radius of the Ferris wheel (r) = 15 metres
Time taken for one revolution (t) = 60 seconds
Substitute the given values into the formula:
v = (2π×15)/60
v = 30π/60
v = 0.5π
Since the value of π is approximately 3.14, we can approximate speed:
v ≈ 0.5 × 3.14
v ≈ 1.57 ms-1
So, the speed of a person sitting on the Ferris wheel at the outer edge is approximately 1.57 ms-1.





