Solved Questions on Quadrilateral
1. Which of the following shows the correct values of unknown angles?
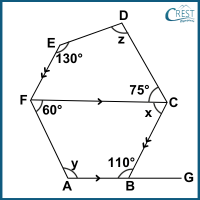
a) x = 70°; y = 120°; z = 75°
b) x = 75°; y = 120°; z = 70°
c) x = 85°; y = 120°; z = 70°
d) x = 70°; y = 120°; z = 85°
Answer: d) x = 70°; y = 120°; z = 85°
Explanation: In trapezium ABCF, AB // CF
x + 110° = 180° [Co-interior angle, AB // CF]
∴ x = 70°
y + 60° = 180° [Co-interior angle, AB // CF]
∴ y = 120°
Since, ∠EFC = x = 70° [Alternate angle, CB || EF]
Sum of interior angles of a quadrilateral DEFC = 360°
⇒ z + 130° + ∠EFC + 75° = 360°
⇒ z + 130° + 70° + 75° = 360°
⇒ z + 275° = 360°
⇒ z = 360° − 275°
∴ z = 85°
Hence, x = 70°, y = 120° and z = 85°.
2. In the adjoining figure, ABCD is a rhombus and CDEF is a square. If ∠ABC = 62°, then what is the size of ∠AEF?
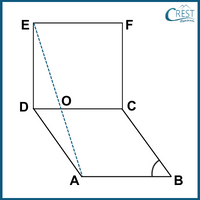
a) 56°
b) 66°
c) 76°
d) 86°
Answer: c) 76°
Explanation: If ABCD is a rhombus, then AB = BC = CD = DA.
If CDEF is a square, then CD = DE = EF = FC.
Hence, AB = BC = CD = DA = DE = EF = FC.
∠ABC = 62° [ Given]
∠ADC = 62° [Opposite angles in a rhombus are equal.]
∠EDC = 90° [Each angle of a square is right angle.]
So, ∠EDA = ∠EDC + ∠ADC = 90° + 62° = 152°
In △AED,
∠DEA = ∠DAE [Angles opposite to equal sides are equal, AD = DE]
Sum of interior angles of a triangle = 180°
⇒ ∠EDA + ∠DEA + ∠DAE = 180°
⇒ 152° + ∠DEA + ∠DEA = 180°
⇒ 2∠DEA = 180° − 152°
⇒ 2∠DEA = 28°
∴ ∠DEA = 14°
∠DEF = 90° [Each angle of a square is right angle.]
⇒ ∠AEF + ∠DEA = 90°
⇒ ∠AEF + 14° = 90°
⇒ ∠AEF = 90° − 14°
∴ ∠AEF = 76°
3. If one angle of a rhombus is 60° and the length of a side is 6 cm, what is the length of the diagonal AC?
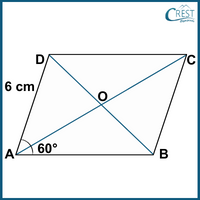
a) 3√2 cm
b) 3√3 cm
c) 6√2 cm
d) 6√3 cm
Answer: d) 6√3 cm
Explanation: ABCD is a rhombus.
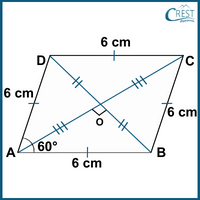
AB = BC = CD = DA = 6 cm [Side of a rhombus.]
∠ A = ∠C = 60° [Opposite angles are equal.]
∠ B = ∠D = 180° − 60° = 120° [Sum of adjacent angles is 180°.]
In △BAD,
∠ A = 60° [Given]
∠ABD = 120°/2 = 60° [BD bisect ∠B.]
∠ADB = 120°/2 = 60° [BD bisect ∠D.]
So, △BAD is an equilateral triangle.
Then, AB = BD = DA = 6 cm
As we know the diagonals of a rhombus bisect each other at right angles.
AO = OC,
BO = OD = 6/2 = 3 cm
∠AOB = 90°
In ∠AOB,
OA2 = AB2 − OB2 [By Pythagoras theorem]
⇒ OA2 = 62 − 32
⇒ OA2 = 36 − 9
⇒ OA2 = 27
⇒ OA = √27
∴ OA = 3√3 cm
AC = 2 × OA = 2 × 3√3 cm = 6√3 cm
∴ The length of the diagonal AC is 6√3 cm.
4. Which of the following quadrilaterals is obtained by joining the mid-points of an isosceles trapezium?
a) Rectangle
b) Rhombus
c) Square
d) Kite
Answer: b) Rhombus
Explanation: ABCD is an isosceles trapezium in which AB || CD and AD = BC. AC and BD are the diagonals of an isosceles trapezium ABCD.
P, Q, R and S are the midpoints of the sides AB, BC, CD and DA.
PQ, QR, RS and SP are joined to form the quadrilateral PQRS.
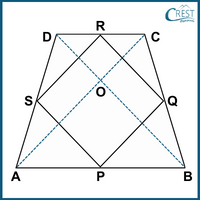
In an isosceles trapezium ABCD, the length of diagonals is equal.
AC = BD
Using the mid-point theorem,
In △ABC,
If P and Q are the midpoints of AB and BC, then PQ || AC and PQ = ½ AC......(I)
In △ADC,
If S and R are midpoints of CD and AD, then SR || AC and SR = ½ AC....(II)
From (I) and (II), PQ || SR and PQ = SR …………..(a)
In △ABD,
If P and S are the midpoints of AB and DA, then PS || BD and PS = ½ BD......(III)
In △BCD,
If Q and R are the midpoints of BC and CD, then QR || BD and QR = ½ BD....(IV)
From (III) and (IV), PS || QR and PS = QR …………..(b)
Thus, PQRS is a parallelogram.
AD = BC
AS = ½ AD = ½ BC = BQ
In △APS and △BPQ,
AP = BP [P is the midpoint.]
∠A = ∠B [Angles opposite to equal sides are equal, AD = BC]
AS = BQ [Found above.]
△APS ≅ △BPQ [By SAS axiom of congruency.]
PS = PQ [By C.P.C.T] …………..(c)
From (a), (b) and (c), the adjacent sides of a parallelogram ABCD are equal.
PQ = SR = PS = QR
No angles of an isosceles trapezium ABCD is 90°. So, PQRS has no right angle.
∴ Hence, all sides of parallelogram PQRS are equal. Therefore, PQRS is a rhombus.
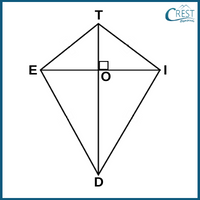
5. What is the difference between ∠DIE and ∠TEO if ∠ITE and ∠IDE of a kite TIDE are 124° and 58°, respectively?
a) 13°
b) 23°
c) 33°
d) 63°
Answer: c) 33°
Explanation: The diagonals of a kite TIDE meet each other at right angles and bisect the angles.
∠IOT = ∠EOT= ∠DOE = ∠DOI = 90°
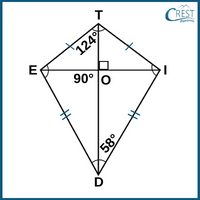
∠ITE = 124°
∠ITO = ∠ETO = ∠ITE/2 = 124°/2 = 62° [Diagonal TD bisects the angles ∠ITE.]
Similarly, ∠IDE = 58°
∠ODI = ∠ODE = ∠IDE/2 = 58°/2 = 29° [Diagonal TD bisects the angles ∠IDE.]
In △IOD,
Sum of interior angles of a triangle = 180°
⇒ ∠DIO + ∠DOI + ∠ETO = 180°
⇒ ∠DIO + 90° + 29° = 180°
⇒ ∠DIO = 61°
∴ ∠DIE = ∠DIO = 61°
In △TOE,
Sum of interior angles of a triangle = 180°
⇒ ∠TEO + ∠TOE + ∠ODI = 180°
⇒ ∠TEO + 90° + 62° = 180°
∴ ∠TEO = 28°
Difference between ∠DIE and ∠TEO = 61° − 28° = 33°








