Solved Questions on Surface Area and Volume
1. Based on the statement, which of the conclusions is valid?
Statement: The inner diameter of a circular well is 4 m and its depth is 17.5 m. The cost of plastering this curved surface area is $8.35 per m2.
Conclusion A: The total cost of plastering is $484.5π.
Conclusion B: The total cost of plastering is $684.5π.
a) Only A
b) Only B
c) Both A and B
d) Neither A nor B
Answer:d) Neither A nor B
Explanation: Radius (r) = ½ × 4 m = 2 m
Depth (h) = 12.5 m
Inner curved surface area of the well (CYLINDER) = 2πrh
= 2 × π × 2 × 17.5
= 70π m2
Total cost of plastering = Area to be plastered × cost of plastering per m2
= 70π × $8.35
= $584.5π
2. What is the volume of the cone that has the same radius and height as that of the cylinder if the volume of a cylinder is 555 cm3?
a) 165 cm3
b) 185 cm3
c) 205 cm3
d) 225 cm3
Answer:b) 185 cm3
Explanation: Volume of cone = ? πr2h = ? × Volume of Cylinder = ? × 555 cm3 = 185 cm3
3. What is the volume of the given figure?
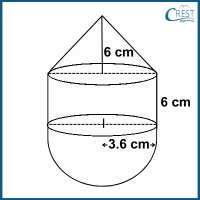
a) (12.96 × 6.4π) cm3
b) (12.96 × 8.4π) cm3
c) (12.96 × 10.4π) cm3
d) (12.96 × 12.4π) cm3
Answer:c) (12.96 × 10.4π) cm3
Explanation: Common radius (r) = 3.6 cm
Height (h) = 6 cm
Total volume of the figure = Volume of cone + Volume of cylinder + Volume of hemisphere
= 1⁄3 πr2h + πr2h + 2⁄3 πr3
= πr2 (1⁄3 h + h + 2⁄3 r)
= π(3.6)2 (1⁄3 × 6 + 6 + 2⁄3 × 3.6)
= π × 12.96 (2 + 6 + 2.4)
= π × 12.96 × (2 + 6 + 2.4)
= π × 12.96 × 10.4
= π × 12.96 × 10.4
= (12.96 × 10.4π) cm3
4. What is the total surface area of the given figure?
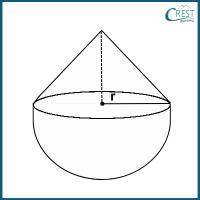
a) √2(1 −√2)πr2 cm2
b) √2(1 + √2)πr2 cm2
c) √2(2 −√2)πr2 cm2
d) √2(2 + √2)πr2 cm2
Answer: b) √2(1 + √2)πr2 cm2
Explanation: Height (h) of the cone = Radius of the cone = r
Slant height (l) of the cone = √(r2 + h2)
= √(r2 + r2)
= √(2r2)
= r√2
Required surface area = Curved surface area of hemisphere + Curved surface area of cone
= 2πr2 + πrl
= 2πr2 + πr × r√2
= 2πr2 + πr2√2
= √2 × √2πr2 + √2πr2
= √2πr2 (√2 + 1)
= √2(1 + √2)πr2 cm2
5. The diameter of Mars is approximately one-fourth of the diameter of Mercury. What fraction of the volume of Mercury is the volume of Mars?
a) 1/8
b) 1/16
c) 1/32
d) 1/64
Answer:d) 1/64
Explanation:





