1. In an experiment, a 2 kg object is released from a height of 5 m. Calculate the potential energy at the release point and the kinetic energy just before hitting the ground.
a) 0 J, 98 J
b) 9.8 J, 9.8 J
c) 98 J, 98 J
d) 98 J, 49 J
Answer: c) Given:
Mass (m) = 2 kg
Height (h) = 5 metres
Acceleration due to gravity (g) = 9.8 m/s2
Potential Energy (PE) at the release point:
Potential energy is given by the formula: PE = m x g x h
Substitute the values:
PE = 2 kg × 9.8 m/s2 × 5 m = 98 J
So, the potential energy at the release point is approximately 98 joules.
Kinetic Energy (K.E.) just before hitting the ground:
All of the potential energy is converted to kinetic energy just before hitting the ground. Therefore, the potential energy at the release point is equal to the kinetic energy just before hitting the ground.
K.E. = 98J
2. A solar panel with a power rating of 300 W generates electricity for 6 hours per day. How much energy does it produce in a week?
a) 1800 Wh
b) 1800 kWh
c) 12.6 kWh
d) 12600 kWh
Answer: c) To calculate the energy produced by the solar panel in a week, we can use the formula:
Energy = Power × Time
Given:
Power (P) = 300 W
Time (t) = 6 hours per day
First, calculate the energy produced in one day:
Energy in one day = Power × Time = 300 W × 6 hours = 1800 Wh (watt-hours)
Now, since there are 7 days in a week, you can calculate the energy produced in a week:
Energy in a week = Energy in one day × Number of days in a week = 1800 Wh × 7 days = 12600 Wh
To express the energy in kilowatt-hours (kWh), divide by 1000:
Energy in a week = 12600 Wh / 1000 = 12.6 kWh
So, the solar panel produces 12.6 kilowatt-hours of energy in a week.
3. A roller coaster starts from a high hill and descends with increasing speed. How does its mechanical energy change over time?
a) Mechanical energy increases.
b) Mechanical energy decreases.
c) Mechanical energy remains constant.
d) Mechanical energy varies randomly.
Answer: c) As the roller coaster descends, its potential energy decreases due to the lowering height, while its kinetic energy increases due to the increasing speed. However, the sum of potential and kinetic energy (mechanical energy) remains constant if no non-conservative forces like friction are acting.
4. Emily and Michael are lifting weights. Emily lifts a weight of 50 kg to a height of 2 metres in 5 seconds. Michael lifts a weight of 70 kg to a height of 3 m in 7 seconds. Whose power output is greater?
a) Emily's
b) Michael's
c) Both have the same power output
d) Cannot be determined from the given information
Answer: b) To compare Emily's and Michael's power outputs, we can use the formula for power:
Power (P) = Work / Time
In this context, the work done is equal to the gravitational potential energy gained by lifting the weights, and the time is the time taken to lift the weights.
For Emily:
Mass (m) = 50 kg
Height (h) = 2 metres
TimeE = 5 s
WorkE = m x g x h
WorkE = 50 kg x 9.81 m/s2 x 2 m = 981 J
PowerE = WorkE / TimeE
PowerE = 981 J / 5 s = 196.2 W
For Michael:
Mass (m) = 70 kg
Height (h) = 3 metres
TimeM = 7 s
WorkM = m x g x h
WorkM = 70 kg x 9.81 m/s2 x 3 m = 2054.7 J
PowerM = WorkM / TimeM
PowerM = 2054.7 J / 7 s = 293.53 W
Comparing the power outputs:
PowerE < PowerM
Therefore, Michael's power output is greater than Emily's.
5. You're pushing a sledge across a frozen pond with a force of 50 N at a 60-degree angle to the ice. If the sledge moves a distance of 10 m, how much work have you done on the sledge?
a) 500 J
b) 250 J
c) 433 J
d) 866 J
Answer: b) Work done on the sledge is 250 J
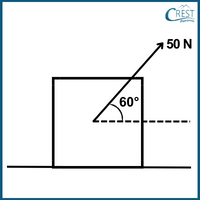
To calculate the work done on the sledge, we need to consider the component of the force that is in the direction of the sledge's motion. This component is given by:
Force in the direction of motion = Force × cos(θ)
Where:
Force is 50 N
θ is the angle of 60 degrees
So, the force component in the direction of motion = 50 N × cos(60o) = 50 N × 0.5 = 25 N
Now, you can calculate the work done using the formula:
Work = (Force in the direction of motion) × Distance
Work = 25 N × 10 m = 250 N m = 250 J
Therefore, the work done on the sledge is 250 (J).


