Volume of Cylinder

Solved Questions of Volume of a Cylinder

1. Find the volume of a hollow cylinder whose outer radius is 5 m, inner radius is 4 m and height is 14 m. (Use π = 22/7).

a) 462 m³
b) 330 m³
c) 450 m³
d) 396 m³

Answer: d) 396 m³

Explanation: V = π (R² - r²) h
= 22/7 (5² - 4²) 14
= 22/7 (25 - 16) 14
= 22/7 x 9 x14
= 396 m³

So, the volume of the cylinder is 396 m³.

2. Find the approximate volume of the cylinder shown:

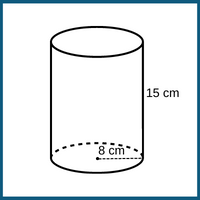
a) 3014 cm³
b) 2099 cm³
c) 1987 cm³
d) 1876 cm³

Answer: a) 3014 cm³

Explanation: V = πr²h
V = (3.14) (8 x 8) (15)
V = 3014.4 cm³

3. The volume of a cylinder is 440 cm³ and the height is 35 cm. Find the radius of the cylinder of a base.

a) 2 cm
b) 3 cm
c) 4 cm
d) 5 cm

Answer: a) 2 cm

Explanation: V = 440 cm³
h = 35 cm
V = πr² h
440 = (22/7) x r² x 35
r² = (440 x 7) / (22 x 35) = 3080/770 = 4
r = 2 cm

4. Calculate volume of the cylinder in which the height is given as 20 cm and the radius of the base is given as 14 cm. (Take π = 22/7)

a) 12320 cm³
b) 23120 cm³
c) 23210 cm³
d) 23201 cm³

Answer: a) 12320 cm³

Explanation: h = 20 cm
r = 14 cm

Volume of the cylinder, V = πr²h
V = (22/7) x 14 x 14 x 20
V = 12320 cm³

5. Calculate the height of a cylinder if its volume is 570 m³ and its radius is 4 m.

a) 11.34 m
b) 10.24 m
c) 9.8 m
d) 8.7 m

Answer: a) 11.34 m

Explanation: We have, V = 570 m³ and r = 4 m
Using the formula we have,
V = πr²h
h = V/πr²
h = 570/ (3.14 × 4 × 4)
h = 11.34 m

Practice Questions of Volume of Cylinder

1. One day, Alex was wondering, “How do I find the volume of a cylinder whose height is 6 inches and radius is 3 inches.” Can you help him to find the volume of that cylinder?

a) 117.22 in³
b) 169.56 in³
c) 198.12 in³
d) 213.06 in³

Answer: b) 169.56 in³

2. A cylinder has a base area equal to 154 m² and a height equal to 4.6 m. find the radius and volume of a cylinder.

a) 2.2 m, 650 m³
b) 7 m, 680.4 m³
c) 14 m, 780.4 m³
d) 7 m, 708.4 m³

Answer: d) 7 m, 708.4 m³ 

3. Find the approximate volume of a cylinder with a radius 5.3 cm and perpendicular height 3.8 cm.

a) 337 cm³
b) 338 cm³
c) 335 cm³
d) 344 cm³

Answer: c) 335 cm³

4. Calculate the radius of a cylinder if its volume is 264 m³ and height is 14 m.

a) √3 m
b) √4 m
c) √5 m
d) √6 m

Answer: d) √6 m

5. Calculate the volume of the figure shown below.

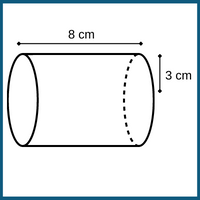
a) 42π cm³
b) 56π cm³
c) 63π cm³
d) 72π cm³

Answer: d) 72π cm³

6. A cylinder has a radius of 6 cm and a height of 8 cm. What is the volume of the cylinder?

a) 288π cm³
b) 148π cm³
c) 288 cm³
d) 148 cm³

Answer: a) 288π cm³

7. The radii of two right circular cylinders are in the ratio 14:3. Find the ratio of their volumes if their heights are in the ratio 9:7.

a) 14/9
b) 28/1
c) 1/2
d) 3/7

Answer: b) 28/1

8. Find the height of the hollow cylinder given that volume = 264 cm³, outer radius = 6 cm and inner radius = 4 cm. (Use π = 22/7)

a) 8 cm
b) 5 cm
c) 4.2 cm
d) 6 cm

Answer: c) 4.2 cm

9. A rectangular sheet of metal foil with dimensions 66 cm x 12 cm is rolled to form a cylinder of height 12 cm. Find the volume of the cylinder.

a) 4158 cm³
b) 3765 cm³
c) 4089 cm³
d) 3981 cm³

Answer: a) 4158 cm³

10. The volume of a cylindrical water tank is 1100 m³ and the radius of the base of the cylindrical tank is 5 m. Calculate the height of the tank.

a) 12 m
b) 14 m
c) 16 m
d) 20 m

Answer: b) 14 m